Identitas Trigonometri

Identitas Trigonometri adalah suatu hubungan atau relasi atau bisa juga dikatakan dengan sebuah kalimat terbuka yang di dalamnya terdapat fungsi-fungsi trigonometri serta bernilai benar untuk setiap pertukaran variabel dengan konstan anggota yang terdapat pada domain fungsinya.

Agar anda bisa memahami identitas trigonometri coba lihat gambar 1 berikut ini

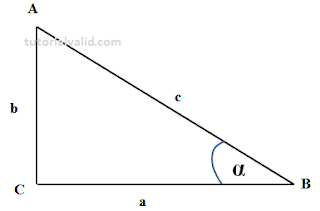Gambar 1 Segitiga Siku Siku

Gambar 1 Merupakan sebuah gambar segitiga siku-siku yang memiliki sudut α sebagai salah satu sudutnya.

Identitas trigonometri dasar

Di mana identitas trigonometri dasar adalah:
sin α = a/c
cos α = b/c
sin α = c/a

cosec α = 1/sin α
sec α = 1/cos α
cot α = 1/tan α


tan α =  sin α/cos α
cot α =  cos α/sin α

Identitas trigonometri phytagoras

Di bawah ini identitas trigonometri phytagoras:
cos² α+ sin² α = 1  

(cos² α+ sin² α)/cos² α = 1/cos² α
(cos² α/cos² α)+ (sin² α/cos² α) = 1/cos² α
1 +  tan² α = sec² α


(cos²α+ sin²α)/sin²α = 1/sin²α
(cos² α/sin²α)+ (sin²α/sin²α) = 1/sin²α
cot²α +  1 = cosec²α

sin(-α) = - sin α
cos(-α) = - cos α
tan(-α) = - tan α

Identitas trigonometri penjumlan sudut

Berikut identitas trigonometri penjumlahan sudut dan perbedaaan sudut (Angle-sum and angle-different):

sin (A + B) = sin A cos B + cos A . sin B
sin (A - B) = sin A cos B - cos A . sin B
cos (A + B) = cos A cos B - sin A . sin B
cos (A - B) = cos A cos B + sin A . sin B

tan (A+B) = 

tan (A-B) =

Identitas trigonometri sudut ganda

Berikut identitas trigonometri sudut ganda (double angle)

sin 2A = 2 sin A. sin B

cos 2A = cos²A -sin²A = 1 - 2sin²A = 2cos²A- 1

Identitas trigonometri sudut setengah

Identitas trigonometri sudut setengah (half angle):

​​

​​​
















Persamaan-persamaan trigonometri di atas dinamakan dengan identitas trigonometri. Dengan menggunakan identitas trigonometri di atas, kita bisa melakukan pembuktian-pembuktian persamaan-persamaan trigonometri yang akan kita lakukan di bawah ini:

1. Buktikan identitas trigonometri berikut
bahwa
identitas trigonometri berikut
 y = sin²α

sama dengan identitas trigonometri berikut
y= (1-cos⁴α)/(1+cos²α).

Jawab

2. Terdapat dua persamaan y1 = (sin²α - sin²β)/(cos²α . cos²β) dan y2 = tan²α . tan²β. Buktikan bahwa y1 = y2.

Jawab:

Jika pada persamaan identitas trigonometri dasar terdapat:

Maka nilai Y menjadi:

Y = (tan² α . sec²β) - (tan² β . sec²α)

Lihat persamaan identitas trigonometri di atas dimana:
1 +  tan² α = sec² α

Maka nilai Y jika dimasukkan persamaan  sec² α menjadi

Y = (tan² α . (1 +  tan² β)) - (tan² β . (1 +  tan² α))
Y = (tan² α  +  tan² α tan² β) - (tan² β  +  tan² β . tan² α
Y = tan² α  +  tan² α tan² β - tan² β  -  tan² β . tan² α

Sehingga terbukti

Y1=Y2 = Y = tan² α - tan² β

Demikianlah artikel dengan judul identitas trigonometri, jika anda memiliki pertanyaan dan masalah tentang identitas trigonometri anda bisa menghubungi kami, terima kasih.

Identitas Trigonometri 2017-08-13T07:50:00+07:00 Rating: 4.5 Diposkan Oleh: Dedy Fermana