Matriks Singular

Matriks Singular. Matriks singular merupakan matriks non-invertible (tidak dibalik). Jadi matriks singular adalah matrik yang jika dibalik (diinvers) tidak dapat dihitung hasilnya.

Kenapa tidak bisa dihitung hasilnya?

Sebuah matriks dikatakan singular atau non-invertable jika matriks tersebut memiliki nilai determinan sama dengan nol.

Jadi jika nilai determinan nol maka invers matriksnya memiliki nilai tidak hingga seperti yang saya jabarkan di bawah ini:

A^-1 = (1/det(A)) * adjoin(A)

Jika det(A)  = 0, Maka:
A^-1 = (1/0) * adjoin(A) = tidak hingga

Dari pembahasan di atas, itulah sebabnya kenapa matriks singular dikatakan sebagai matriks yang memiliki nilai determinan sama dengan nol, hal itu karena matriks tersebut akan menghasilkan nilai matriks invers menjadi tidak berhingga (invers tidak berhingga).

Sebelum membahas tentang matriks singular lebih lanjut. Ada baiknya terlebih dahulu membahas tentang dasar matriks terlebih dahulu.

Karena jika kita belum menguasai tentang dasar matriks maka nantinya akan kesulitan menyelesaikan persoalan matriks singular.

Sebelum memulai dasar matriks ada hal yang perlu anda ketahui tentang aljabar linier.

Aljabar Linier merupakan salah satu cabang ilmu matematika yang penting untuk dipelajari.

Aljabar linier ini memiliki hubungan dengan persamaan linier, vektor serta vektor ruang.

Kebanyakan semua aljabar linier itu menggunakan konsep matriks.

Sebuah matriks dikatakan berbentuk persegi panjang jika memiliki baris dan kolom.

Setiap baris dan kolom tersebut berisi angka atau variabel yang dikenal dengan unsur-unsur atau  isian-isian.

Jumlah baris dan kolom yang terdapat dalam matrik mewakili ukuran atau dimensi dari matriks tersebut

Gambar 1 Matriks m x n

Sekarang kita misalkan

A dan B adalah matriks bujur sangkar n x n yang memenuhi kondisi antara lain:

AB = I = BA

Yang mana I adalah identitas dari matriks yang memiliki orde n x n.

A merupakan matrik non-singular dan B merupakan invers (kebalikan) dari matriks A.

Matriks A bisa dikatakan sebagai matriks singular jika ia memenuhi keadaan determinan menghasilkan nilai nol (0).

det (A) = 0 atau |A| = 0

Dimana:
|A| = det(A)

Determinan matriks singular

Setiap matriks persegi pasti mempunyai sebuah determinan.

Determinan secara nyata (aktual) merupakan sebuah konsep dalam matematika yang mempunyai peran penting dalam menyelesaikan sebuah analisis dari sebuah sistem persamaan linear.

Jika anda ingin mengetahui lebih dalam tentang determinan matriks anda bisa mengunjungi halaman kami yang membahas tentang determinan matriks.

Mari kita lihat bentuk matrik 2x2 di bawah ini

Gambar 2 Matriks 2x2

Gambar 2 adalah gambar matriks 2x2. Bagaimana menyelesaikan determinan dari matrik 2x2 di atas? Determinan A atau |A| adalah:

|A| = (a.d) - (b.c)

Untuk detail bagaimana mencari rumus determinan anda bisa melihat link pada halaman paling bawah bagaimana mencari determinan.

Jika hasil dari sebuah determinan matriks sama dengan 0, maka matriks tersebut dikatakan matriks singular.

det (A) = 0

Jadi untuk matriks 2x2, rumus untuk membuktikan bahwa matriks tersebut singular atau non-singular adalah

|A| = (a.d) - (b.c) = 0

Marilah kita bahas contoh 1 di bawah ini yang menentukan apakah matriks-matriks di bawah ini adalah merupakan matriks singular atau matriks non-singular.

Contoh 1.

Diketahui matriks di bawah ini adalah matriks 2x2, tentukan apakah matriks -matriks dibawah ini singular atau non-singular

Matriks A.

Gambar 3 Matriks A

Matrik B

Gambar 4 Matriks B

Jawaban:

Matriks A.
Baiklah kita bahas dari Matriks A

Dari gambar 2 didapatkan rumus determinan matriks orde 2x2 yaitu
|A| = (a.d) - (b.c)

Maka:
|A| = (2.3) - (6.1) = (6) - (6) = 0

Syarat Matriks dikatakan singular adalah |A| = 0
Dari hasil yang didapatkan Matriks A adalah Matriks Singular


Matriks B
|B| = (a.d) - (b.c) = (5.3) - (2.6) = (15) - (12) = 3

Syarat singular adalah |B| = 0

Dari hasil perhitungan Matriks B adalah Matriks non-singular 

Dari 2 contoh matriks 2x2 di atas, tampak bahwa matriks A adalah matrik singular dan matriks B adalah matriks non-singular.

Kenapa jika determinan sebuah matriks memiliki nilai nol (0) disebut matriks singular?

Baiklah, marilah kita pahami konsep di bawah secara detail

Seperti yang kita ketahui bahwa invers dari sebuah matrik A adalah sebagai berikut:

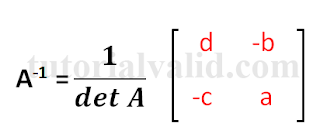Gambar 5 Invers Matriks A

Tampak dari gambar 5, jika nilai determinan A adalah 0 maka hasil invers adalah tidak hingga (hasil invers  tidak akan bisa di cari).

Itulah sebabnya kenapa matriks dengan nilai determinan sama dengan nol (0) dikatakan matriks singular karena matriks singular tidak bisa diinverskan.

Mari kita lihat struktur dari matrik 3x3 di bawah ini

Gambar 6 Matriks 3x3

Gambar 6 adalah gambar matriks 3x3. Bagaimana menyelesaikan determinan dari matrik 3x3 di atas? Determinan atau |A| matriks 3x3 adalah

|A| = a((e.i) - (f.h))  - b((d.i) - (f.g)) + c((d.h)-(e.g))

Bagaimana mencari rumus determinan sebuah matriks?

Anda bisa melihat link berikut determinan matriks, saya terlah menulis pada halaman tersebut bagaimana menentukan rumus determinan.

Jika hasil dari determinan dari matriks 3x3 adalah sama dengan 0, maka matriks 3x3 tersebut dapat dikatakan matriks singular jika:

|A| = 0

Jadi pada matriks 3x3, rumus untuk menentukan bahwa matriks tersebut adalah matriks singular atau non-singular adalah

|A| = a((e.i) - (f.h))  - b((d.i) - (f.g)) + c((d.h)-(e.g)) = 0

Marilah kita coba membahas contoh 2 di bawah ini apakah matriks singular atau matriks non-singular.

Contoh 2.

Diketahui matriks-matriks di bawah ini adalah matriks 3x3, buktikan apakah matriks -matriks di bawah ini merupakan matriks singular atau non-singular

Matriks C.

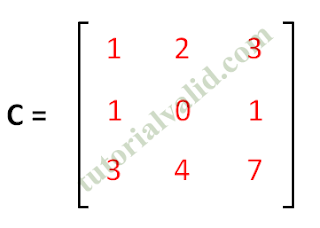Gambar 7 Matriks C 3x3

Matriks D

Gambar 8 Matriks D 3x3

Jawaban:

Lihat gambar 7 Matriks C.
Baiklah kita bahas Matriks C

Dari gambar 6 di dapat persamaan rumus determinan matriks 3x3 adalah
|C| = a((e.i) - (f.h))  - b((d.i) - (f.g)) + c((d.h)-(e.g))

Maka:
|C| = 1((0.7) - (1.4))  - 2((1.7) - (1.3)) + 3((1.4)-(0.3)) = 1(0-4) - 2(7-3) + 3(4-0)
|C| = 1(-4)   - 2(4) + 3(4) = -4 -8 + 12 = 0
Syarat Matriks dikatakan singular adalah |C| = 0
Dari hasil yang didapatkan bahwa Matriks C ordo 3x3 adalah Matriks Singular


Lihat gambar 8 Matriks D
Dari gambar 6 maka persamaan rumus determinan matriks 3x3 adalah
|D| = a((e.i) - (f.h))  - b((d.i) - (f.g)) + c((d.h)-(e.g))

Maka:
|D| = 8((3.1) - (1.-2))  - -3((4.1) - (0.1)) + 2((4.-2)-(3.0)) = 8(3+2) + 3(4-0) + 2(-8-3)
|D| = 8(5)   + 3(4) + 2(-11) = 40 +12 - 22 = 30

Syarat Matriks dikatakan singular adalah jika |D| = 0
Dari hasil yang didapatkan Matriks D = 30  jadi Matriks D merupakan matriks non-singular

Setelah pembahasan dan soal yang saya berikan di atas tentang bagaimana menentukan matriks singular. Saya berharap anda dapat menentukan mana matriks singular dan yang mana matriks non-singular.

Bagaimana mencari rumus determinan sebuah matrik?

Anda bisa mengunjungi halaman tutorial kami tentang determinan matriks.

Pada halaman tersebut saya akan membahas bagaimana mencari determinan sebuah matriks ber orde 2x2, 3x3 dan 4x4 sehingga anda bisa menyelesaikan berapapun determinan sebuah orde matriks, terima kasih.

Matriks Singular 2016-11-14T15:01:00+07:00 Rating: 4.5 Diposkan Oleh: Dedy Fermana