Determinan Matriks. Determinan Matriks adalah sebuah nilai yang didapatkan dari sebuah matriks persegi yang mana nilai tersebut nantinya digunakan untuk mencari nilai dari invers sebuah matriks.
Determinan sebuah matriks hanya bisa didapatkan dari sebuah matriks persegi.
Determinan ini digunakan juga untuk menyelesaikan sebuah persamaan linier. Sebuah persamaan jika nilai determinannya menghasilkan 0 maka dinamakan matriks singular.
Determinan sebuah matriks hanya bisa didapatkan dari sebuah matriks persegi.
Determinan ini digunakan juga untuk menyelesaikan sebuah persamaan linier. Sebuah persamaan jika nilai determinannya menghasilkan 0 maka dinamakan matriks singular.
Pada artikel berikut saya akan menjelaskan bagaimana menentukan determinan sebuah matriks baik matriks tersebut berordo 2x2, atau 3x3 maupun 4x4.
Determinan yang saya jelaskan di bawah juga akan diberikan contoh soal bagaimana menyelesaikan sebuah matriks.
Dengan penjelasan saya di bawah, diharapakan anda bisa memahami dan menyelesaikan determinan dari matriks dengan berbagai orde.
Determinan yang saya jelaskan di bawah juga akan diberikan contoh soal bagaimana menyelesaikan sebuah matriks.
Dengan penjelasan saya di bawah, diharapakan anda bisa memahami dan menyelesaikan determinan dari matriks dengan berbagai orde.
Notasi Determinan dari matriks.
Pada pelajaran matematika biasanya notasi dari determinan matriks ditulis dengan:
det(?)
atau:
|?|
Tanda tanya (?) diisi identitas dari sebuah matriks.
Jika matriks tersebut adalah matriks A maka notasi determinan matriks tersebut adalah det(A) atau |A|.
Jika matriks tersebut adalah matriks B maka determinannya adalah det(B) atau |B|.
Jika matriks tersebut adalah matriks A maka notasi determinan matriks tersebut adalah det(A) atau |A|.
Jika matriks tersebut adalah matriks B maka determinannya adalah det(B) atau |B|.
Baiklah, sekarang kita akan memulai bagaimana menentukan determinan matriks menggunakan metoda minor cofactors dan Metoda Ekspansi Laplace
Determinan Matriks 2x2
Determinan Matriks 2x2 bisa anda lihat pada gambar 1 di bawah ini: |
| Gambar 1 Matriks 2x2 |
Pada matriks A 2x2 yang anda lihat pada gambar 1.
Matriks tersebut memiliki elemen a, b c dan d.
Untuk menyelesaikan matriks ini anda bisa menggunakan metoda cofactors.
Penggunaan metoda cofactors ini memberikan tanda pada matriks berupa tanda min dan plus.
Pada baris pertama kita bisa memberikan tanda plus terlebih dahulu kemudian min dan seterusnya bergantian (jika matriks memiliki orde yang lebih dari dua).
Dan baris kedua dimulai dari min kemudian berikutnya plus dan seterusnya bergantian.
Pemberian tanda plus terlebih dahulu kemudian bergantian tanda min.
Begitulah penggunaan metoda cofactors. Pemberian tanda cofactor bisa anda lihat pada gambar 2 berikut:
Matriks tersebut memiliki elemen a, b c dan d.
Untuk menyelesaikan matriks ini anda bisa menggunakan metoda cofactors.
Penggunaan metoda cofactors ini memberikan tanda pada matriks berupa tanda min dan plus.
Pada baris pertama kita bisa memberikan tanda plus terlebih dahulu kemudian min dan seterusnya bergantian (jika matriks memiliki orde yang lebih dari dua).
Dan baris kedua dimulai dari min kemudian berikutnya plus dan seterusnya bergantian.
Pemberian tanda plus terlebih dahulu kemudian bergantian tanda min.
Begitulah penggunaan metoda cofactors. Pemberian tanda cofactor bisa anda lihat pada gambar 2 berikut:
 |
| Gambar 2 Matriks 2x2 dengan tanda cofactors |
Setelah menetukan tanda kurang dan tambah (min dan plus) seperti gambar 2 barulah kita menentukan determinan dengan aturan yang terlihat pada gambar.
Ingat tanda kurang dan tambah digunakan untuk menentukan koofesien matriks apakah min atau plus.
Berikut gambar 3 aturan determinan.
Ingat tanda kurang dan tambah digunakan untuk menentukan koofesien matriks apakah min atau plus.
Berikut gambar 3 aturan determinan.
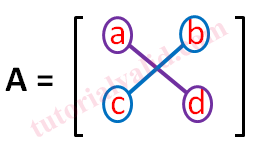 |
| Gambar 3 Aturan determinan matriks 2x2 |
Lihat pada gambar 3 terdapat elemen matriks dengan warna ungu dan biru.
Jika kita kaitkan dengan gambar 2 tanda minus dan tanda plus maka elemen a bertanda plus dan elemen b bertanda minus.
Tiap warna menandakan bahwa elemen matriks tersebut dikali. Jadi hasil dari determinan matriks A adalah
Jika kita kaitkan dengan gambar 2 tanda minus dan tanda plus maka elemen a bertanda plus dan elemen b bertanda minus.
Tiap warna menandakan bahwa elemen matriks tersebut dikali. Jadi hasil dari determinan matriks A adalah
det(A) = |A| = + (a.d) - (b.c)
Demikianlah determinan dari matriks dengan orde 2x2.
Determinan Matriks 3x3
Setelah membahas bagaimana menentukan determinan dari matriks 3x3, kita akan kembali mempelajari bagaimana menentukan matriks dengan orde 3x3.
Untuk penyelesaiannya kita tetap menggunakan metoda cofactors. Anda bisa melihat gambar 4 di bawah, gambar matriks 3x3.
Untuk penyelesaiannya kita tetap menggunakan metoda cofactors. Anda bisa melihat gambar 4 di bawah, gambar matriks 3x3.
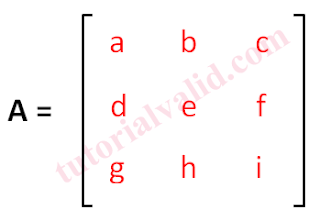 |
| Gambar 4 Matriks 3x3 |
Untuk menyelesaikan matrik 3x3 di atas (gambar 4), tetap menggunakan metoda cofactors dengan memberikan tanda kurang dan tambah (min dan plus) pada elemen-elemen yang terdapat pada matriks 3x3 di atas. Berikut pemberian tanda kurang dan tambah lihat gambar 5.
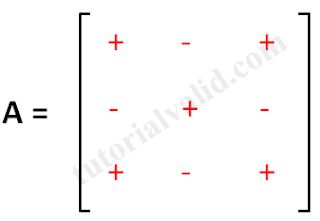 |
| Gambar 5 Matriks 3x3 dengan tanda cofactors |
Pemberian tanda tetap bergantian untuk tiap elemen dari matriks.
Namun pemberian tanda dimulai pada elemen pertama dengan tanda plus (tambah).
Namun pemberian tanda dimulai pada elemen pertama dengan tanda plus (tambah).
Kemudian kita memulai aturan determinan matriks menggunakan metoda ekspansi laplace.
Setiap elemen matriks pada baris petama harus dihitung untuk mendapatkan determinan matriks A, kita mulai dari elemen a, kemudian b dan kemudian c.
Agar lebih mudah mengerti anda bisa melihat warna-warna yang terdapat pada setiap elemen pada matriks
1. Elemen a
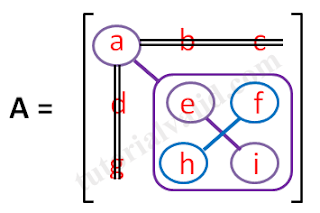 |
| Gambar 6 Elemen a pada matriks 3x3 |
Tanda garis dua berwarna hitam pada gambar 6 berarti elemen tersebut dicoret atau tidak diikutkan dalam perhitungan. Elemen yang tidak diikutkan dalam perhitungan adalah b,c,d,g.
Pada elemen a mendapat tanda tambah (plus) lihat gambar 5 sehingga didapatkan persamaan:
+ a ((e.i)-(f.h))
2. Elemen b (lihat gambar 7)
 |
| Gambar 7 Matriks 3x3 elemen b |
Tanda garis dua berwarna hitam pada gamber 7 berarti elemen tersebut dicoret atau tidak diikutkan dalam perhitungan.
Elemen yang tidak diikutkan dalam perhitungan adalah a,c,e,h.
Pada elemen b mendapat tanda min (kurang) lihat gambar 5 sehingga didapatkan persamaan:
- b ((d.i)-(f.g))
3. Elemen c (lihat gambar 8)
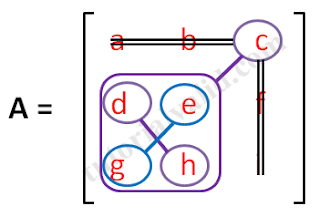 |
| Gambar 8 Matriks 3x3 elemen c |
Pada gambar 8 di dapatkan:
Tanda garis dua berwarna hitam pada gamber 8 berarti elemen tersebut dicoret atau tidak diikutkan dalam perhitungan.
Elemen yang tidak diikutkan dalam perhitungan adalah a,b,f,i.
Pada elemen c mendapat tanda tambah (plus) lihat gambar 5 sehingga dapat persamaan:
+ c ((d.h)-(e.g))
Dari tiga persamaan elemen a, elemen b dan elemen c jika digabungkan akan menhasilkan determinan
det(A) = |A| = + a ((e.i)-(f.h)) - b ((d.i)-(f.g)) + c ((d.h)-(e.g)) = a.e.i - a.f.h - b.d.i + b.f.g + c.d.h -c.e.g
Demikianlah penjabaran dari determinan matrik 3x3
Determinan Matriks 4x4
Setelah membahas bagaimana mencari determinan dari matriks 3x3, kita akan kembali memahami bagaimana menentukan matriks dengan orde 4x4.
Kita menggunakan metoda cofactors untuk mencari determinan matrik orde 4x4.
Anda bisa melihat gambar 9 di bawah ini, gambar 9 tersebut merupakan bentuk dari matriks 4x4.
Kita menggunakan metoda cofactors untuk mencari determinan matrik orde 4x4.
Anda bisa melihat gambar 9 di bawah ini, gambar 9 tersebut merupakan bentuk dari matriks 4x4.
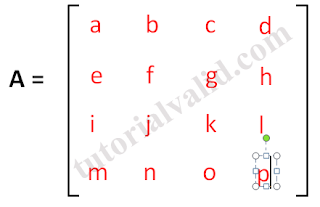 |
| Gambar 9 Matriks 4x4 |
Untuk menyelesaikan matrik 4x4 di atas (gambar 9), kita akan menggunakan
metoda cofactors dengan memberikan tanda tambah dan kurang (plus dan minus) pada elemen-elemen (a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p) yang terdapat pada matriks 4x4 di atas .
Berikut pemberian tanda kurang dan tambah yang bisa dilihat pada gambar 10.
Berikut pemberian tanda kurang dan tambah yang bisa dilihat pada gambar 10.
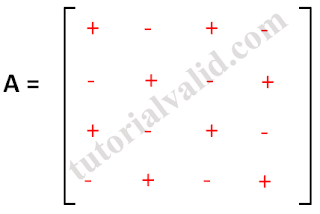 |
| Gambar 10 Matriks 4x4 dengan tanda cofactors |
Penyelesaian matriks 4x4, kita kelompokkan menjadi 4 kelompok, yaitu:
Kelompok 1 elemen a.
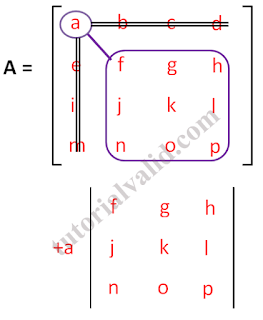 |
| Gambar 11 Matriks 4x4 kelompok 1 elemen a |
Pada kelompok 1 ketika kita mengambil elemen a untuk diproses, setelah memproses elemen a yang mana elemen a bertanda tambah (plus sesuai aturan cofactors) maka akan terdapat matriks 3x3 yang harus dikalikan dengan a (lihat gambar 11). Matriks 3x3 dengan elemen f,g,h,j,k,l,n,o,p bisa diselesaikan melalui cara yang telah kita lakukan sebelumnya, berikut penyelesaiannya lihat gambar 12
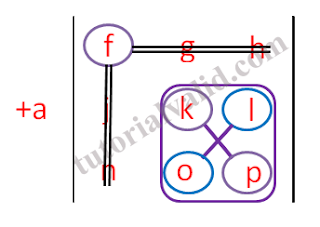 |
| Gambar 12 Kelompok 1 elemen a dengan matriks 3x3 |
(+a).((+f).((k.p)-(l.o))) = +a.f.k.p -a.f.l.o ....persamaan(1)
Anda dapat meneruskannya untuk elemen g pada kelompok 1 elemen a dengan menggunakan penyelesaian matriks 3x3 untuk elemen a yang telah saya jelaskan di atas.
(+a).((-g).((j.p)-(l.n))) = -a.g.j.p + a.g.l.n ....persamaan(2)
Anda dapat meneruskannya untuk elemen h pada kelompok 1 elemen a dengan menggunakan penyelesaian matriks 3x3 yang telah saya jelaskan di atas.
(+a).((+h).((j.o)-(k.n))) = +a.h.j.o - a.h.k.n .....persamaan(3)
Kelompok 2 elemen b.
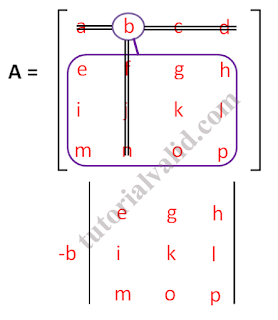 |
| Gambar 13 Matriks 4x4 kelompok 2 elemen b |
Dari gambar 13 matriks 4x4 kelompok 2 elemen b didapatkan persamaan
(-b).((+e).((k.p) - (l.o)) = -b.e.k.p + b.e.l.o ....persamaan(4)
(-b).((-g).((i.p) - (l.m)) = +b.g.i.p - b.g.l.m ....persamaan(5)
(-b).((+h).((i.o) - (k.m)) = -b.h.i.o + b.h.k.m ....persamaan(6)
Kelompok 3 elemen c dapat anda lihat pada gambar 14 di bawah ini
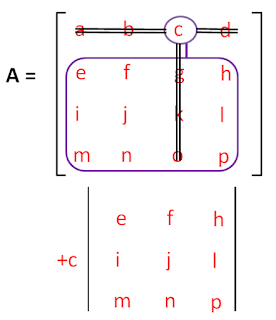 |
| Gambar 14 Matriks 4x4 Kelompok 3 elemen c |
Dari gambar 14 matriks 4x4 kelompok 3 elemen c didapatkan persamaan
(+c).((+e).((j.p) - (l.n)) = +c.e.j.p - c.e.l.n .....persamaan(7)
(+c).((-f).((i.p) - (l.m)) = -c.f.i.p + c.f.l.m ....persamaan(8)
(+c).((+h).((i.n) - (j.m)) = +c.h.i.n - c.h.j.m ....persamaan(9)
Kelompok 4 elemen d dapat anda lihat pada gambar 15 di bawah ini
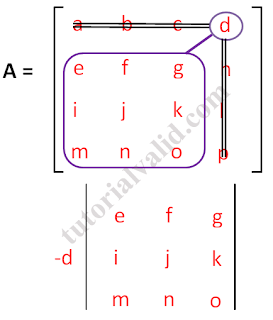 |
| Gambar 15 Matriks 4x4 kelompok 4 elemen d |
Dari gambar 15 matriks 4x4 kelompok 4 elemen d didapatkan persamaan
(-d).((+e).((j.o) - (k.n)) = -d.e.j.o + d.e.k.n ....persamaan(10)
(-d).((-f).((i.o) - (k.m)) = +d.f.i.o - d.f.k.m ....persamaan(11)
(-d).((+g).((i.n) - (j.m)) = -d.g.i.n + d.g.j.m ....persamaan(12)
Dari ke 12 persamaan tersebut maka didapatkan nilai determinan A
| det(A)=|A|= | persaman 1 + persamaan 2 + persamaan 3 + persamaan 4 + persamaan 5 + persamaan 6 + persaman 7 + persamaan 8 + persamaan 9 + persamaan 10 + persamaan 11 + persamaan 12 |
jadi :
| det(A)=|A|= | +a.f.k.p - a.f.l.o - a.g.j.p + a.g.l.n + a.h.j.o - a.h.k.n - b.e.k.p + b.e.l.o + b.g.i.p - b.g.l.m -b.h.i.o + b.h.k.m + c.e.j.p - c.e.l.n - c.f.i.p + c.f.l.m + c.h.i.n - c.h.j.m - d.e.j.o + d.e.k.n + d.f.i.o - d.f.k.m -d.g.i.n + d.g.j.m |
| det(A )= |A| = | +a.f.k.p + a.g.l.n +a.h.j.o |
| +b.e.l.o +b.g.i.p + b.h.k.m | |
| +c.e.j.p + c.f.l.m +c.h.i.n | |
| + d.e.k.n +d.f.i.o + d.g.j.m | |
| -a.f.l.o -a.g.j.p - a.h.k.n | |
| -b.e.k.p - b.g.l.m -b.h.i.o | |
| -c.e.l.n -c.f.i.p - c.h.j.m | |
| -d.e.j.o - d.f.k.m -d.g.i.n |
Untuk melengkapi pemahaman tentang determinan matriks, saya akan memberikan beberapa contoh soal yang terkait dengan matriks 2x2, 3x3 dan 4x4.
Contoh soal determinan matriks
Tentukan determinan dari matriks matriks di bawah ini.1.Tentukan determinan dari matriks B 2x2 di bawah ini
2. Tentukan determinan matriks D 3x3 di bawah ini
3.Berapakah determinan matriks A 4x4 di bawah ini
Jawab
1. Untuk matriks B 2x2 kita bisa mengambil rumus yang telah kita tentukan di atas:
det(A) = |A| = + (a.d) - (b.c)
Di mana dari matriks 2x2 pada soal jika dikonversi ke gambar 1 maka diketahui nilai:
a = 12, b = 16, c = -9, d = 3
Maka:
det(B) = |B| = + (12.3) - (16. -9) = + (36) - (-144) = 36 + 144 = 180
Jadi determinan untuk matriks B adalah 180
2. Untuk matriks D 3x3 pada soal di atas bisa kita cari dengan rumus berikut
det(A) = |A| = + a ((e.i)-(f.h)) - b ((d.i)-(f.g)) + c ((d.h)-(e.g)) = a.e.i - a.f.h - b.d.i + b.f.g + c.d.h -c.e.g
Di mana dari matriks 3x3 yang terdapat pada soal jika dikonversi ke gambar4 maka nilai:
a = 9 , b = -7 , c = 8, d = 3, e = 5, f = 2, g = 6, h = -2, i = -5
Maka determinan matriks D adalah
det(D) = |D| = (a.e.i) - (a.f.h) - (b.d.i) + (b.f.g) + (c.d.h) -(c.e.g)
det(D) = |D| = (9.5.-5) - (9.2.-2) - (-7.3.-5) + (-7.2.6) + (8.3.-2) -(8.5.6)
det(D) = |D| = (-225) - (-36) - (105) + (-84) + (-48) - (240) = -666
Hasil dari determinan matriks D adalah - 666
3. Untuk matriks A 4x4 pada soal di atas bisa kita dapatkan dengan rumus berikut
| det(A )= |A| = | +a.f.k.p + a.g.l.n +a.h.j.o |
| +b.e.l.o +b.g.i.p + b.h.k.m | |
| +c.e.j.p + c.f.l.m +c.h.i.n | |
| + d.e.k.n +d.f.i.o + d.g.j.m | |
| -a.f.l.o -a.g.j.p - a.h.k.n | |
| -b.e.k.p - b.g.l.m -b.h.i.o | |
| -c.e.l.n -c.f.i.p - c.h.j.m | |
| -d.e.j.o - d.f.k.m -d.g.i.n |
Di mana dari matriks yang terdapat pada soal jika dikonversi ke gambar 9 maka nilai:
a = 8 , b = 0 , c = 8, d = 4, e = 7, f = 3, g = 6, h = 9, i = -9, j = 2, k = -5 , l = 7, m = -3, n=7, o=3, p=2
Maka determinan matriks A adalah
| det(A )= |A| = | + (8.3.-5.2) + (8.6.7.7) + (8.9.2.3) |
| + (0.7.7.3) + (0.6.-9.2) + (0.9.-5.-3) | |
| + (8.7.2.2) + (8.3.7.-3) + (8.9.-9.7) | |
| + (4.7.-5.7) + (4.3.-9.3) + (4.6.2.-3) | |
| - (8.3.7.3) - (8.6.2.2) - (8.9.-5.7) | |
| - (0.7.-5.2) - (0.6.7.-3) -(0.9.-9.3) | |
| - (8.7.7.7) - (8.3.-9.2) - (8.9.2.-3) | |
| - (4.7.2.3) - (4.3.-5.-3) -(4.6.-9.7) |
| det(A)=|A|= | + (-240) + (2352) + (432) + (0) + (0) + (0) + (224) + (-504) + (-4536) + (-980) + (-324) + (-144) - (504) - (192) - (-2520) - (0) - (0) - (0) - (2744) - (-432) - (-432) - (168) - (180) - (1512) |
det(A) = |A| = -5636
Hasil dari determinan matriks D 4x4 adalah -5636
Demikianlah artikel determinan matriks.
Diharapkan anda dapat mengerti bagaimana mencari determinan matriks dengan ordo berapapun, terima kasih.





0 komentar:
Post a Comment
Note: Only a member of this blog may post a comment.