Transpose Matriks

Transpose Matriks adalah melakukan transpose terhadap matriks, yang mana baris dan kolom dari suatu matriks kita tukar letaknya. Pada transpose matriks, baris yang terdapat pada matriks menjadi kolom. sedangkan kolom pada matriks menjadi baris.

Transpose matriks merupakan salah satu dari pelajaran matematika yang berhubungan dengan matriks.

Transpose matriks ini digunakan jika anda ingin menginverskan sebuah matriks (lihat invers matriks).

Maksud dari menukar letak dari baris dan kolom adalah baris pertama dari matriks tersebut di letak ke kolom pertama, baris kedua pada matriks diletakkan ke kolom kedua dan baris ketiga dari matriks diletakkan ke kolom ke tiga, untuk lebih jelasnya anda bisa melihat gambaran dari transpose matriks pada gambar 1.

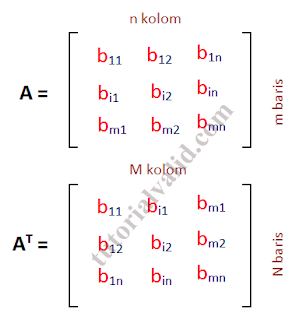Gambar 1 Transpose Matriks

Dari gambar 1 di atas tampak bahwa m baris menjadi n baris dan n kolom menjadi m kolom.

Dari gambar 1 bisa dilihat bahwa baris pertama yaitu b₁₁, b₁₂ dan b_1n menjadi kolom pertama.

Baris kedua yaitu b_i1, b_i2 dan b_in menjadi kolom kedua. Baris ketiga yaitu b_m1, b_m2 dan b_mn menjadi kolom ketiga.

Sehingga jika dilihat pada A^T (A transpose) baris pertama menjadi b₁₁, b_i1 dan b_m1.

Baris kedua menjadi b₁₂, b_i2 dan b_m2. Baris ketiga menjadi b_1n, b_in dan b_mn

Adapun sifat dari transpose matriks dalam perhitungan matriks adalah sebagai berikut:

• (AB)^T = B^T . A^T
• λ(A^T) = (λA^T)        Dimana λ adalah scalar
• (A + B)^T = A^T + B^T
• (A^T)^T = A

Untuk melengkapi pemahaman anda dalam mempelajari transpose matriks, saya akan memberikan contoh soal beserta pembahasan yang berhubungan dengan transpose matrik.

Contoh Soal Transpose Matriks dan Pembahasan

Soal 1

 Tentukan matriks transpose dari matriks-matriks yang terdapat di bawah ini

Gambar 2 Matriks 2x2

A. Berapakah Transpose matriks dari Matriks B ordo 2x2 pada gambar 2 di atas?

Gambar 3 Matriks 3x3

B. Tentukan matriks transpose dari Matriks D dengan ordo 3x3 yang terdapat pada gambar 3 di atas.

Gambar 4 Matriks 4x4

C. Cari matriks transpose dari matriks A dengan ordo 4x4 seperti yang terdapat pada gambar 4 di atas.

Jawaban:

Soal 1 A. Untuk soal 1 A Jika diketahui matriks 2x2 seperti gambar 2 bagaimana transpose matriksnya?

Seperti yang telah kita baca bahwa baris ditukar tempat dengan kolom maka jawabannya adalah:

Gambar 5 Jawaban Soal 1 A

Pada soal 1A baris pertama (12,16) dan baris kedua (-9 3). jika kita transpose maka baris tersebut kita jadikan kolom (baris pertama menjadi kolom pertama, baris kedua menjadi kolom kedua).

Tampak dari gambar 5 hasil dari transpose adalah baris pertama (12, -9) dan baris kedua (16,3)

Soal 1 B. Diketahui matriks D 3x3 seperti gambar 3. Di tanya Transpose matriks tersebut

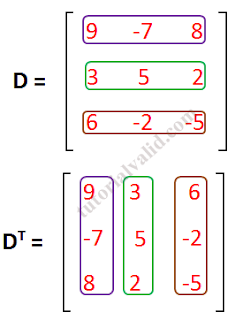Gambar 6 Matriks 3x3 transpose

Pada gambar 3 Sebelum matrik D 3x3 ditranspose terdapat matriks memiliki 3 baris yang mana, lihat gambar 6 pada baris pertama elemen anggota matriks tersebut (9,-7,8) berwarna ungu, baris kedua dari matriks D tersebut adalah (3,5,2) berwarna hijau dan baris ketiga dari matriks D tersebut adalah (6,-2,-5) berwarna coklat. Setelah ditukar letak dari baris menjadi kolom Matriks D^T yang dapat anda lihat pada gambar 6 menghasilkan baris pertama (9,3,6) dan baris kedua menjadi (-7,5,-2) dan baris ketiga menjadi (8,2,-5)

1 C. Diketahui matriks A 4x4 seperti gambar 4. Di tanya Transpose matriks A tersebut adalah

Gambar 7 Matriks 4x4 Transpose

Pada gambar 4 Sebelum matrik A 4x4 ditranspose, matriks A tersebut memiliki 4 baris yang mana dapat anda lihat pada gambar 6, pada baris pertama elemen anggota matriks tersebut (8,0,8,4), baris kedua dari matriks A tersebut adalah (7,3,6,9), baris ketiga dari matriks A tersebut adalah (-9,2,-5,7) dan baris ke empat(-3,7,3,2). Setelah ditukar letak dari baris menjadi kolom maka Matriks A^T (Matriks A Transpose)yang dapat anda lihat pada gambar 7.

Demikianlah Tulisan saya tentang transpose Matriks. Semoga tulisan saya yang membahas tentang transpose matriks dapat anda mengerti, terima kasih

Transpose Matriks 2016-11-16T16:36:00+07:00 Rating: 4.5 Diposkan Oleh: Dedy Fermana